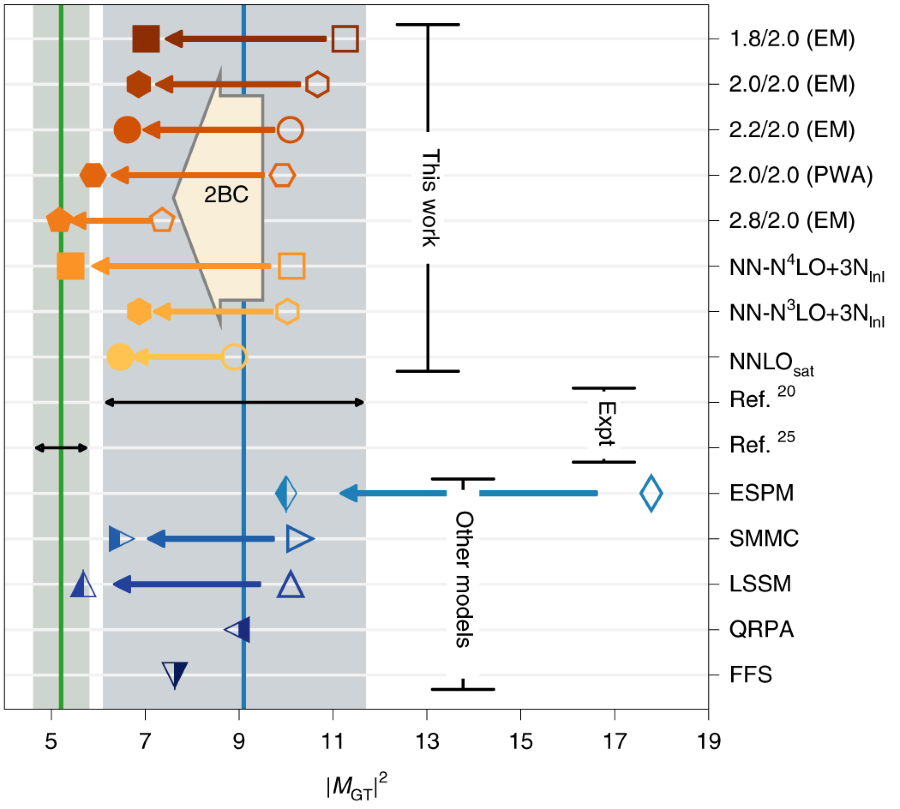
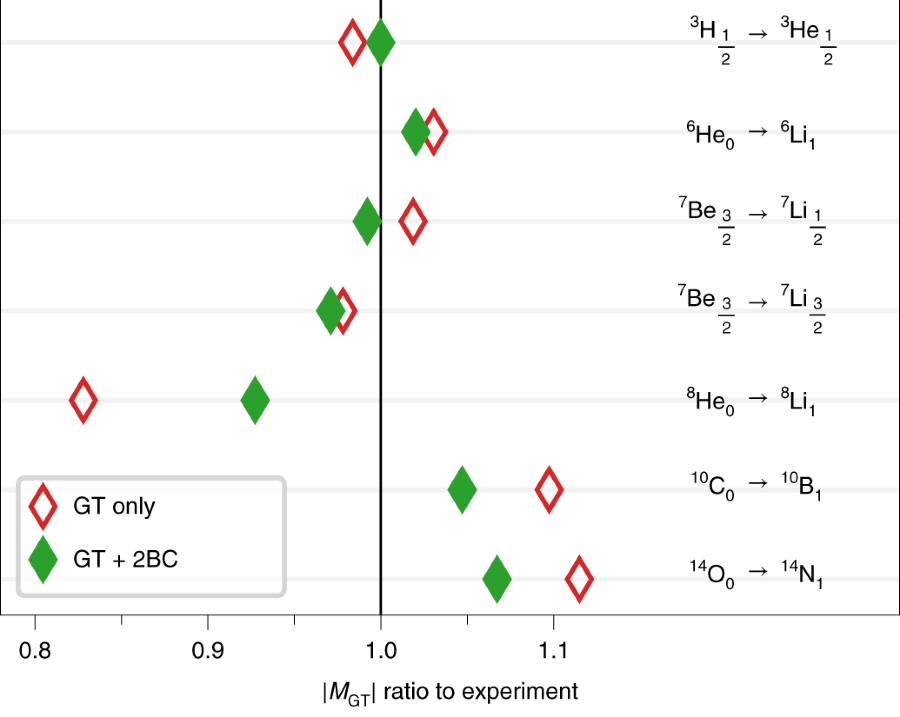
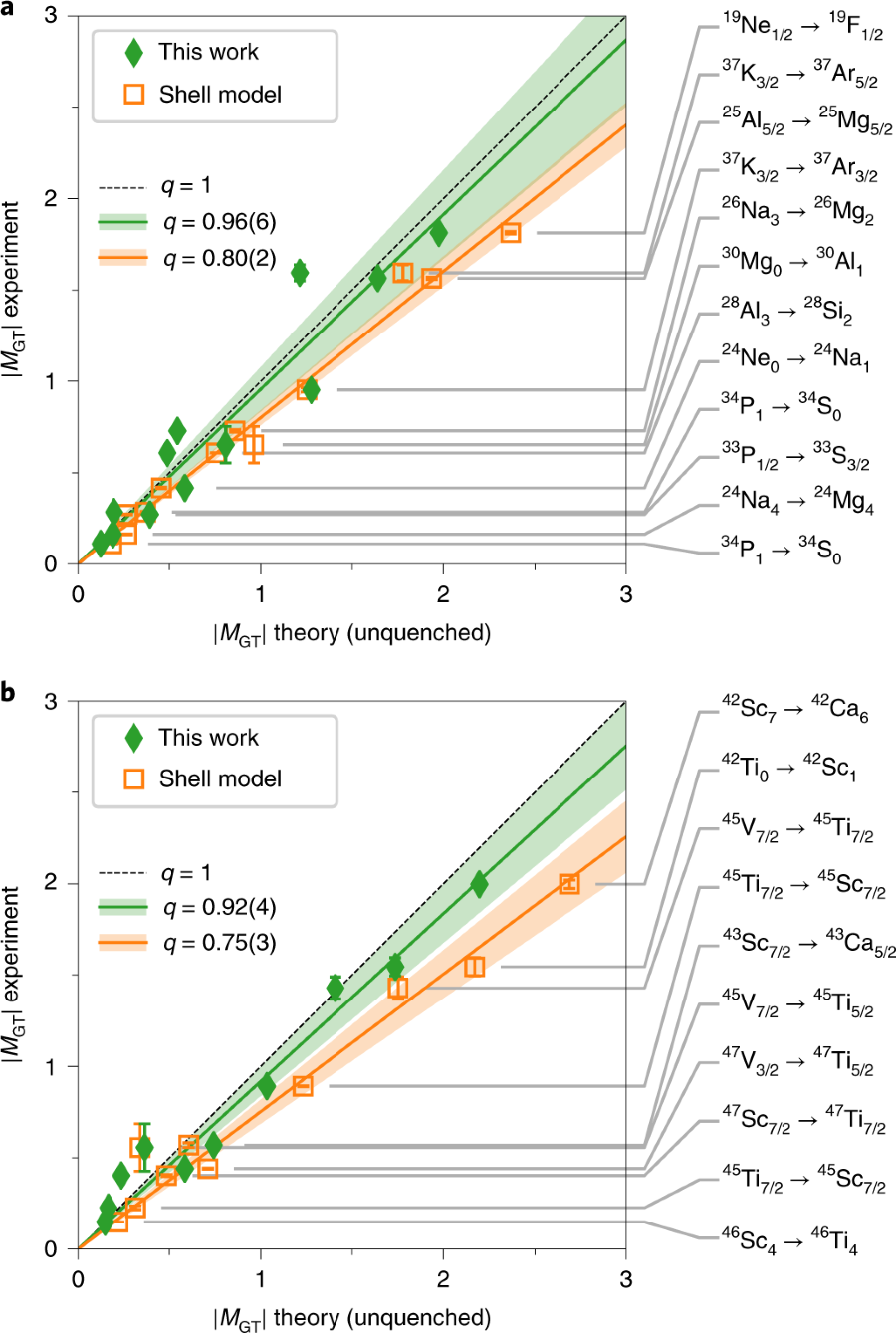
β -decay, a process that changes a neutron into a proton (and vice versa), is the dominant decay mode of atomic nuclei. This decay offers a unique window to physics beyond the standard model, and is at the heart of microphysical processes in stellar explosions and the synthesis of the elements in the Universe. For 50 years, a central puzzle has been that observed β-decay rates are systematically smaller than theoretical predictions. This was attributed to an apparent quenching of the fundamental coupling constant gA≃ 1.27 in the nucleus by a factor of about 0.75 compared to the β-decay of a free neutron. The origin of this quenching is controversial and has so far eluded a first-principles theoretical understanding. Here we address this puzzle and show that this quenching arises to a large extent from the coupling of the weak force to two nucleons as well as from strong correlations in the nucleus. We present state-of-the-art computations of β-decays from light to heavy nuclei. Our results are consistent with experimental data, including the pioneering measurement for 100Sn. These theoretical advances are enabled by systematic effective field theories of the strong and weak interactions combined with powerful quantum many-body techniques. This work paves the way for systematic theoretical predictions for fundamental physics problems. These include the synthesis of heavy elements in neutron star mergers and the search for neutrino-less double-β-decay, where an analogous quenching puzzle is a major source of uncertainty in extracting the neutrino mass scale.

Effective Hamiltonians and effective electroweak operators are calculated with the Okubo-Lee-Suzuki formalism for two-nucleon systems. Working within a harmonic oscillator basis, first without and then with a confining harmonic oscillator trap, we demonstrate the effects of renormalization on observables calculated for truncated basis spaces. We illustrate the renormalization effects for the root-mean-square point-proton radius, electric quadrupole moment, magnetic dipole moment, Gamow-Teller transition and neutrinoless double-beta decay operator using nucleon-nucleon interactions from chiral Effective Field Theory. Renormalization effects tend to be larger in the weaker traps and smaller basis spaces suggesting applications to heavier nuclei with transitions dominated by weakly-bound nucleons would be subject to more significant renormalization effects within achievable basis spaces.

We use a reference state based on symmetry-restored states from deformed mean-field or generator-coordinate-method (GCM) calculations in conjunction with the in-medium similarity-renormalization group (IMSRG) to compute spectra and matrix elements for neutrinoless double-beta (0νββ) decay. Because the decay involves ground states from two nuclei, we use evolved operators from the IMSRG in one nucleus in a subsequent GCM calculation in the other. We benchmark the resulting IMSRG+GCM method against complete shell-model diagonalization for both the energies of low-lying states in 48Ca and 48Ti and the 0νββ matrix element for the decay of 48Ca, all in a single valence shell. Our approach produces better spectra than either the IMSRG with a spherical-mean-field reference or GCM calculations with unevolved operators. For the 0νββ matrix element the improvement is slight, but we expect more significant effects in full ab-initio calculations.

We show that the measured intrinsic octupole moments of \(^{220}\)Rn, \(^{224}\)Ra, and \(^{226}\)Ra constrain the intrinsic Schiff moments of \(^{225}\)Ra, \(^{221}\)Rn, \(^{223}\)Rn, \(^{223}\)Fr, \(^{225}\)Ra, and \(^{229}\)Pa. The result is a dramatically reduced uncertainty in intrinsic Schiff moments. Direct measurements of octupole moments in odd nuclei will reduce the uncertainty even more. The only significant source of nuclear-physics error in the laboratory Schiff moments will then be the intrinsic matrix elements of the time-reversal non-invariant interaction produced by CP-violating fundamental physics. Those matrix elements are also correlated with octupole moments, but with a larger systematic uncertainty.

We present a complete calculation of nucleon-deuteron scattering as well as ground and low-lying excited states of light nuclei in the mass range A=3-16 up through next-to-next-to-leading order in chiral effective field theory using semilocal coordinate-space regularized two- and three-nucleon forces. It is shown that both of the low-energy constants entering the three-nucleon force at this order can be reliably determined from the triton binding energy and the differential cross section minimum in elastic nucleon-deuteron scattering. The inclusion of the three-nucleon force is found to improve the agreement with the data for most of the considered observables.

We present an approach to derive effective shell-model interactions from microscopic nuclear forces. The similarity-transformed coupled-cluster Hamiltonian decouples the single-reference state of a closed-shell nucleus and provides us with a core for the shell model. We use a second similarity transformation to decouple a shell-model space from the excluded space. We show that the three-body terms induced by both similarity transformations are crucial for an accurate computation of ground and excited states. As a proof of principle we use a nucleon-nucleon interaction from chiral effective field theory, employ a 4He core, and compute low-lying states of 6−8He and 6−8Li in p-shell model spaces. Our results agree with benchmarks from full configuration interaction.

We present a master formula describing the neutrinoless-double-beta decay (0νββ) rate induced by lepton-number-violating (LNV) operators up to dimension nine in the Standard Model Effective Field Theory. We provide an end-to-end framework connecting the possibly very high LNV scale to the nuclear scale, through a chain of effective field theories. Starting at the electroweak scale, we integrate out the heavy Standard Model degrees of freedom and we match to an SU(3)c⊗U(1)em effective theory. After evolving the resulting effective Lagrangian to the QCD scale, we use chiral perturbation theory to derive the lepton-number-violating chiral Lagrangian. The chiral Lagrangian is used to derive the two-nucleon 0νββ transition operators to leading order in the chiral power counting. Based on renormalization arguments we show that in various cases short-range two-nucleon operators need to be enhanced to leading order. We show that all required nuclear matrix elements can be taken from existing calculations. Our final result is a master formula that describes the 0νββ rate in terms of phase-space factors, nuclear matrix elements, hadronic low-energy constants, QCD evolution factors, and high-energy LNV Wilson coefficients, including all the interference terms. Our master formula can be easily matched to any model where LNV originates at energy scales above the electroweak scale. As an explicit example, we match our formula to the minimal left-right-symmetric model in which contributions of operators of different dimension compete, and we discuss the resulting phenomenology.

The axial coupling of the nucleon, \(g_A\), is the strength of its coupling to the weak axial current of the Standard Model of particle physics, in much the same way as the electric charge is the strength of the coupling to the electromagnetic current. This axial coupling dictates the rate at which neutrons decay to protons, the strength of the attractive long-range force between nucleons and other features of nuclear physics. Precision tests of the Standard Model in nuclear environments require a quantitative understanding of nuclear physics rooted in Quantum Chromodynamics, a pillar of the Standard Model. The prominence of \(g_A\) makes it a benchmark quantity to determine theoretically - a difficult task because quantum chromodynamics is non-perturbative, precluding known analytical methods. Lattice Quantum Chromodynamics provides a rigorous, non-perturbative definition of quantum chromodynamics that can be implemented numerically. It has been estimated that a precision of two percent would be possible by 2020 if two challenges are overcome: contamination of \(g_A\) from excited states must be controlled in the calculations and statistical precision must be improved markedly. Here we report a calculation of \(g^{QCD}_A=1.271\pm 0.013\), using an unconventional method inspired by the Feynman-Hellmann theorem that overcomes these challenges.

We examine the leading effects of two-body weak currents from chiral effective field theory on the matrix elements governing neutrinoless double-β decay. In the closure approximation these effects are generated by the product of a one-body current with a two-body current, yielding both two- and three-body operators. When the three-body operators are considered without approximation, they quench matrix elements by about 10%, less than suggested by prior work, which neglected portions of the operators. The two-body operators, when treated in the standard way, can produce somewhat larger quenching. In a consistent effective field theory, however, these two-body effects become divergent and must be renormalized by a contact operator, the coefficient of which we cannot determine at present.

Observation of neutrinoless double beta decay, a lepton number violating process that has been proposed to clarify the nature of neutrino masses, has spawned an enormous world-wide experimental effort. Relating nuclear decay rates to high-energy, beyond the Standard Model (BSM) physics requires detailed knowledge of non-perturbative QCD effects. Using lattice QCD, we compute the necessary matrix elements of short-range operators, which arise due to heavy BSM mediators, that contribute to this decay via the leading order \(\pi^-\rightarrow\pi^+\) exchange diagrams. Utilizing our result and taking advantage of effective field theory methods will allow for model-independent calculations of the relevant two-nucleon decay, which may then be used as input for nuclear many-body calculations of the relevant experimental decays. Contributions from short-range operators may prove to be equally important to, or even more important than, those from long-range Majorana neutrino exchange.

Nuclear structure and reaction theory are undergoing a major renaissance with advances in many- body methods, strong interactions with greatly improved links to Quantum Chromodynamics (QCD), the advent of high performance computing, and improved computational algorithms. Predictive power, with well-quantified uncertainty, is emerging from non-perturbative approaches along with the potential for new discoveries such as predicting nuclear phenomena before they are measured. We present an overview of some recent developments and discuss challenges that lie ahead. Our focus is on explorations of alternative truncation schemes in the harmonic oscillator basis, of which our Japanese–United States collaborative work on the No-Core Monte-Carlo Shell Model is an ex- ample. Collaborations with Professor Takaharu Otsuka and his group have been instrumental in these developments.

Matter effects on the mixing of the neutrinos mass eigenstates, also know as the Mikheyev-Smirnov-Wolfenstein effect, seem to be well established in describing the propagation of the neutrino from the source to detecting devices. These effects were mostly considered in bulk matter, but not inside the atoms. Here we consider the effect of the high electron densities existing in the atomic nuclei. We investigate if these effects can affect the known neutrino phenomenology. It was reported that the mixing of the neutrino in high density matter, such as inside a supernova, can affect the Majoron decay probabilities. We investigate if the neutrino mixing effects in the high electron density inside the atomic nuclei can change the neutrinoless double beta decay half-life formula. In both cases we found that the standard results stand. The results look simple, but the road to them is complex and it opens the possibility that the neutrino mixing in atomic nuclei may affect other observables, such as the neutrinoless double beta Majoron decays.

Within the framework of chiral effective field theory we discuss the leading contributions to the neutrinoless double-beta decay transition operator induced by light Majorana neutrinos. Based on renormalization arguments in both dimensional regularization with minimal subtraction and a coordinate-space cutoff scheme, we show the need to introduce a leading-order short-range operator, missing in all current calculations. We discuss strategies to determine the finite part of the short-range coupling by matching to lattice QCD or by relating it via chiral symmetry to isospin-breaking observables in the two-nucleon sector. Finally, we speculate on the impact of this new contribution on nuclear matrix elements of relevance to experiment.

We employ a variety of ab initio methods, including Faddeev-Yakubovsky equations, no-core configuration interaction approach, coupled-cluster theory, and in-medium similarity renormalization group, to perform a comprehensive analysis of the nucleon-deuteron elastic and breakup reactions and selected properties of light and medium-mass nuclei up to 48Ca using the recently constructed semilocal coordinate-space regularized chiral nucleon-nucleon potentials. We compare the results with those based on selected phenomenological and chiral EFT two-nucleon potentials, discuss the convergence pattern of the chiral expansion, and estimate the achievable theoretical accuracy at various chiral orders using an approach to quantify truncation errors of the chiral expansion without relying on cutoff variation. We also address the robustness of this method and explore alternative ways to estimate the theoretical uncertainty from the truncation of the chiral expansion.

Weak interaction in nuclei represents a well-known venue for testing many of the fundamental symmetries of the Standard Model. In particular, neutrinoless double-β decay offers the possibility to test beyond Standard Model theories predicting that neutrinos are Majorana fermions and the lepton number conservation is violated. This paper focuses on an effective field theory approach to neutrinoless double-β decay for extracting information regarding the properties of the beyond Standard Model Lagrangian responsible for this process. We use shell model nuclear matrix elements and the latest experimental lower limits for the half-lives to extract 12 lepton-number-violating parameters of five nuclei of experimental interest and lower limits for the energy scales of the new physics. Using the most stringent limits that we obtain for the values of the lepton-number-violating parameters, we predict new half-life limits for the other nuclei of experimental interest, in the case of 12 neutrino double-β decay mechanisms. We provide an analysis that could reveal valuable information regarding the dominant neutrinoless double-β decay mechanism, if experimental half-life data become available for different isotopes.

We present the first ab initio calculations of neutrinoless double beta decay matrix elements in A=6-12 nuclei using Variational Monte Carlo wave functions obtained from the Argonne v18 two-nucleon potential and Illinois-7 three-nucleon interaction. We study both light Majorana neutrino exchange and potentials arising from a large class of multi-TeV mechanisms of lepton number violation. Our results provide benchmarks to be used in testing many-body methods that can be extended to the heavy nuclei of experimental interest. In light nuclei we have also studied the impact of two-body short range correlations and the use of different forms for the transition operators, such as those corresponding to different orders in chiral effective theory.

We present the first chiral effective theory derivation of the neutrinoless double beta-decay \(nn\rightarrow pp\) potential induced by light Majorana neutrino exchange. The effective-field-theory framework has allowed us to identify and parameterize short- and long-range contributions previously missed in the literature. These contributions can not be absorbed into parameterizations of the single nucleon form factors. Starting from the quark and gluon level, we perform the matching onto chiral effective field theory and subsequently onto the nuclear potential. To derive the nuclear potential mediating neutrinoless double beta-decay, the hard, soft and potential neutrino modes must be integrated out. This is performed through next-to-next-to-leading order in the chiral power counting, in both the Weinberg and pionless schemes. At next-to-next-to-leading order, the amplitude receives additional contributions from the exchange of ultrasoft neutrinos, which can be expressed in terms of nuclear matrix elements of the weak current and excitation energies of the intermediate nucleus. These quantities also control the two-neutrino double beta-decay amplitude. Finally, we outline strategies to determine the low-energy constants that appear in the potentials, by relating them to electromagnetic couplings and/or by matching to lattice QCD calculations.

We present a generator-coordinate method for realistic shell-model Hamiltonians that closely approximates the full shell model calculations of the matrix elements for the neutrinoless double-beta decay of 124Sn, 130Te, and 136Xe. We treat axial quadrupole deformations and also triaxial quadrupole deformations, including the proton-neutron pairing amplitudes as generator coordinates. We validate this method by calculating and comparing spectroscopic quantities with the exact shell model results. A detailed analysis of the 0νββ decay nuclear matrix elements for 124Sn, 130Te, and 136Xe is presented. Our Hamiltonian-based generator-coordinate method produces 0νββ matrix elements much closer to the shell model ones, when compared to the existing energy density functional-based approaches. The remaining overestimation of 0νββ nuclear matrix element suggests that additional correlations may be needed to be taken into account for 124Sn, 130Te, and 136Xe when calculating with the Hamiltonian-based generator-coordinate method.

We analyze neutrinoless double beta decay (0νββ) within the framework of the Standard Model Effective Field Theory. Apart from the dimension-five Weinberg operator, the first contributions appear at dimension seven. We classify the operators and evolve them to the electroweak scale, where we match them to effective dimension-six, -seven, and -nine operators. In the next step, after renormalization group evolution to the QCD scale, we construct the chiral Lagrangian arising from these operators. We develop a power-counting scheme and derive the two-nucleon 0νββ currents up to leading order in the power counting for each lepton-number-violating operator. We argue that the leading-order contribution to the decay rate depends on a relatively small number of nuclear matrix elements. We test our power counting by comparing nuclear matrix elements obtained by various methods and by different groups. We find that the power counting works well for nuclear matrix elements calculated from a specific method, while, as in the case of light Majorana neutrino exchange, the overall magnitude of the matrix elements can differ by factors of two to three between methods. We calculate the constraints that can be set on dimension-seven lepton-number-violating operators from 0νββ experiments and study the interplay between dimension-five and -seven operators, discussing how dimension-seven contributions affect the interpretation of 0νββ in terms of the effective Majorana mass mββ.

Background: The interacting boson model (IBM) has been used extensively to calculate the matrix elements governing neutrinoless double-beta decay. Studies within other models indicate that a good description of neutron-proton pairing is essential for accurate calculations of those matrix elements. The usual interacting boson model is based only on like-particle pairs, however, and the extent to which it captures neutron-proton pairing is not clear. Purpose: To determine whether neutron-proton pairing should be explicitly included as neutron-proton bosons in IBM calculations of neutrinoless double-beta decay matrix elements. Method: An isospin-invariant version of the nucleon-pair shell model is applied to carry out shell-model calculations in a large space and in a collective subspace, and to define effective operators in the latter. A democratic mapping is then used to define corresponding boson operators for the IBM, with and without an isoscalar neutron-proton pair boson. Results: IBM calculations with and without the isoscalar boson are carried out for nuclei near the beginning of the pf shell, with a realistic shell-model Hamiltonian and neutrinoless double-beta-decay operator as the starting point. Energy spectra and double-beta matrix elements are compared to those obtained in the underlying shell model. Conclusions: The isoscalar boson does not improve energy spectra but does improve double-beta matrix elements. To be useful at the level of precision we need, the mapping procedure must be further developed to better determine the dependence of the boson Hamiltonian and decay operator on particle number and isospin. But the benefits provided by the isoscalar boson suggest that through an appropriate combination of mappings and fitting, it would make IBM matrix elements more accurate for the heavier nuclei used in experiments.

We use the generator-coordinate method with realistic shell-model interactions to closely approximate full shell-model calculations of the matrix elements for the neutrinoless double-beta decay of \(^{48}\)Ca, \(^{76}\)Ge, and \(^{82}\)Se. We work in one major shell for the first isotope, in the \(f_{5/2}pg_{9/2}\) space for the second and third, and finally in two major shells for all three. Our coordinates include not only the usual axial deformation parameter β, but also the triaxiality angle γ and neutron-proton pairing amplitudes. In the smaller model spaces our matrix elements agree well with those of full shell-model diagonalization, suggesting that our Hamiltonian-based GCM captures most of the important valence-space correlations. In two major shells, where exact diagonalization is not currently possible, our matrix elements are only slightly different from those in a single shell.

Neutrinoless double-beta decay, if observed, would signal physics beyond the Standard Model that would be discovered at energies significantly lower than those at which the relevant degrees of freedom can be excited. Accurate nuclear structure calculation of the nuclear matrix elements (NME) necessary to analyze the decay rates could be helpful to narrow down the list of competing mechanisms, and to better identify the more exotic properties of the neutrinos. In this paper we present and analyze the status of the NME shell model calculations, and their relevance for discriminating the possible competing mechanisms that may contribute to the neutrinoless double-beta decay process.

Recent trends in the analyses of neutrino oscillations and cosmological data suggest that the neutrino mass hierarchy is likely to be normal. This development has consequences for the neutrinoless double beta decay, namely it is more likely to have competition between the standard mass mechanism and other beyond Standard Model mechanisms that may appear above TeV scale. Here we discuss some venues of distinguishing between these potentially competing mechanisms based on shell model nuclear matrix elements.

We present a generator-coordinate method for realistic shell-model Hamiltonians that closely approximates the full shell model calculations of the matrix elements for the neutrinoless double-beta decay of 124Sn, 130Te, and 136Xe. We treat axial quadrupole deformations and also triaxial quadrupole deformations, including the proton-neutron pairing amplitudes as generator coordinates. We validate this method by calculating and comparing spectroscopic quantities with the exact shell model results. A detailed analysis of the 0νββ decay nuclear matrix elements for 124Sn, 130Te, and 136Xe is presented. Our Hamiltonian-based generator-coordinate method produces 0νββ matrix elements much closer to the shell model ones, when compared to the existing energy density functional-based approaches. The remaining overestimation of 0νββ nuclear matrix element suggests that additional correlations may be needed to be taken into account for 124Sn, 130Te, and 136Xe when calculating with the Hamiltonian-based generator-coordinate method.

We report on a lattice QCD calculation of the nucleon axial charge, \(g_A\), using Möbius Domain-Wall fermions solved on the dynamical \(N_f=2+1+1\) HISQ ensembles after they are smeared using the gradient-flow algorithm. The calculation is performed with three pion masses, \(m_\pi\sim{310,220,130}\) MeV. Three lattice spacings (\(a\sim{0.15,0.12,0.09}\) fm) are used with the heaviest pion mass, while the coarsest two spacings are used on the middle pion mass and only the coarsest spacing is used with the near physical pion mass. On the \(m_\pi\sim220\) MeV, \(a\sim0.12\) fm point, a dedicated volume study is performed with \(m_\pi L\sim{3.22,4.29,5.36}\). Using a new strategy motivated by the Feynman-Hellmann Theorem, we achieve a precise determination of \(g_A\) with relatively low statistics, and demonstrable control over the excited state, continuum, infinite volume and chiral extrapolation systematic uncertainties, the latter of which remains the dominant uncertainty. Our final determination at 2.6% total uncertainty is \(g_A=1.278(21)(26)\), with the first uncertainty including statistical and systematic uncertainties from fitting and the second including model selection systematics related to the chiral and continuum extrapolation. The largest reduction of the second uncertainty will come from a greater number of pion mass points as well as more precise lattice QCD results near the physical pion mass.

We report on salient features of a mixed lattice QCD action using valence Möbius domain-wall fermions solved on the dynamical \(N_f=2+1+1\) HISQ ensembles generated by the MILC Collaboration. The approximate chiral symmetry properties of the valence fermions are shown to be significantly improved by utilizing the gradient-flow scheme to first smear the HISQ configurations. The greater numerical cost of the Möbius domain-wall inversions is mitigated by the highly efficient QUDA library optimized for NVIDIA GPU accelerated compute nodes. We have created an interface to this optimized QUDA solver in Chroma. We provide tuned parameters of the action and performance of QUDA using ensembles with the lattice spacings \(a\simeq{0.15,0.12,0.09}\) fm and pion masses \(m_\pi \simeq{310,220,130}\) MeV. We have additionally generated two new ensembles with \(a\sim0.12\) fm and \(m_\pi \simeq{400,350}\) MeV. With a fixed flow-time of \(t_{gf}=1\) in lattice units, the residual chiral symmetry breaking of the valence fermions is kept below 10\% of the light quark mass on all ensembles, \(m_{res}\leq0.1\times m_l\), with moderate values of the fifth dimension \(L_5\) and a domain-wall height \(M_5\leq 1.3\). As a benchmark calculation, we perform a continuum, infinite volume, physical pion and kaon mass extrapolation of \(F_{K_\pm}/F_{\pi_\pm}\) and demonstrate our results are independent of flow-time, and consistent with the FLAG determination of this quantity at the level of less than one standard deviation.

Neutrinoless double-beta decay is proposed as an important low energy phenomenon that could test beyond the Standard Model physics. There are several potentially competing beyond the Standard Model mechanisms that can induce the process. It thus becomes important to disentangle the different processes. In the present study we consider the interference effect between the light left-handed and heavy right-handed Majorana neutrino exchange mechanisms. The decay rate, and consequently, the phase-space factors for the interference term are derived, based on the left–right symmetric model. The numerical values for the interference phase-space factors for several nuclides are calculated, taking into consideration the relativistic Coulomb distortion of the electron wave function and finite-size of the nucleus. The variation of the interference effect with the Q -value of the process is studied.

TeV-scale lepton number violation can affect neutrinoless double beta decay through dimension-9 ΔL=ΔI=2 operators involving two electrons and four quarks. Since the dominant effects within a nucleus are expected to arise from pion exchange, the π−→π+ee matrix elements of the dimension-9 operators are a key hadronic input. In this letter we provide estimates for the π−→π+ matrix elements of all Lorentz scalar ΔI=2 four-quark operators relevant to the study of TeV-scale lepton number violation. The analysis is based on chiral SU(3) symmetry, which relates the π−→π+ matrix elements of the ΔI=2 operators to the K0→K¯0 and K→ππ matrix elements of their ΔS=2 and ΔS=1 chiral partners, for which lattice QCD input is available. The inclusion of next-to-leading order chiral loop corrections to all symmetry relations used in the analysis makes our results robust at the 30% level or better, depending on the operator.

We present a precise lattice QCD calculation of the contribution to the neutron-proton mass splitting arising from strong isospin breaking, mn−mp|QCD=2.32±0.17 MeV. We also determine mΞ−−mΞ0|QCD=5.44±0.31 MeV. The calculation is performed at three values of the pion mass, with several values of the quark mass splitting and multiple lattice volumes, but only a single lattice spacing and an estimate of discretization errors. The calculations are performed on the anisotropic clover-Wilson ensembles generated by the Hadron Spectrum Collaboration. The omega-baryon mass is used to set the scale a−1t=6111±127 MeV, while the kaon masses are used to determine the value of the light-quark mass spitting. The nucleon mass splitting is then determined as a function of the pion mass. We observe, for the first time, conclusive evidence for non-analytic light quark mass dependence in lattice QCD calculations of the baryon spectrum. When left as a free parameter, the fits prefer a nucleon axial coupling of gA=1.24(56). To highlight the presence of this chiral logarithm in the nucleon mass splitting, we also compute the isospin splitting in the cascade-baryon system which is less sensitive to chiral dynamics. Finally, we update the best lattice QCD determination of the CP-odd pion-nucleon coupling that would arise from a non-zero QCD theta-term, g¯0/(2‾√fπ)=(14.7±1.8±1.4)⋅10−3θ¯. The original lattice QCD correlation functions, analysis results and extrapolated quantities are packaged in HDF5 files made publicly available including a simple Python script to access the numerical results, construct effective mass plots along with our analysis results, and perform the extrapolations of various quantities determined in this work.

The Feynman-Hellmann theorem can be derived from the long Euclidean-time limit of correlation functions determined with functional derivatives of the partition function. Using this insight, we fully develop an improved method for computing matrix elements of external currents utilizing only two-point correlation functions. Our method applies to matrix elements of any external bilinear current, including nonzero momentum transfer, flavor-changing, and two or more current insertion matrix elements. The ability to identify and control all the systematic uncertainties in the analysis of the correlation functions stems from the unique time dependence of the ground-state matrix elements and the fact that all excited states and contact terms are Euclidean-time dependent. We demonstrate the utility of our method with a calculation of the nucleon axial charge using gradient-flowed domain-wall valence quarks on the \(N_f=2+1+1\) MILC highly improved staggered quark ensemble with lattice spacing and pion mass of approximately 0.15 fm and 310 MeV respectively. We show full control over excited-state systematics with the new method and obtain a value of \(g_A=1.213(26)\) with a quark-mass-dependent renormalization coefficient.

The nuclear matrix elements that govern the rate of neutrinoless double beta decay must be accurately calculated if experiments are to reach their full potential. Theorists have been working on the problem for a long time but have recently stepped up their efforts as ton-scale experiments have begun to look feasible. Here we review past and recent work on the matrix elements in a wide variety of nuclear models and discuss work that will be done in the near future. Ab initio nuclear-structure theory, which is developing rapidly, holds out hope of more accurate matrix elements with quantifiable error bars.

Neutrinoless double-beta decay is a predicted beyond Standard Model process that could clarify some of the not yet known neutrino properties, such as the mass scale, the mass hierarchy, and its nature as a Dirac or Majorana fermion. Should this transition be observed, there are still challenges in understanding the underlying contributing mechanisms. We perform a detailed shell model investigation of several beyond Standard Model mechanisms that consider the existence of right-handed currents. Our analysis presents different venues that can be used to identify the dominant mechanisms for nuclei of experimental interest in the mass region (\(^{124}\)Sn, \(^{130}\)Te, and \(^{136}\)Xe). It requires accurate knowledge of nine nuclear matrix elements that we calculate in addition to the associated energy-dependent phase space factors.